Inversion swapping two circles

Consider two circles \(\mathcal{C}_1(O_1,r_1)\) and \(\mathcal{C}_2(O_2,r_2)\). There is always an inversion which swaps \(\mathcal{C}_1\) and \(\mathcal{C}_2\) (which maps \(\mathcal{C}_1\) to \(\mathcal{C}_2\) and \(\mathcal{C}_2\) to \(\mathcal{C}_1\)). When this is an inversion on a circle, this circle of inversion is called a mid-circle of \(\mathcal{C}_1\) and \(\mathcal{C}_2\).

Congruent case

When \(r_1 = r_2\), the two circles \(\mathcal{C}_1\) and \(\mathcal{C}_2\) can be swapped by an inversion on a line (that is, a reflection with respect to this line); obviously, this line is the perpendicular bisector of the segment joining the two centers \(O_1\) and \(O_2\). We could say that this line is a mid-circle, if we allow the mid-circle to be a generalized circle.

If the two circles are tangent, this is the unique mid-circle.

When \(r_1 = r_2\), the two circles \(\mathcal{C}_1\) and \(\mathcal{C}_2\) can be swapped by an inversion on a circle if they intersect each other at two points. The pole of this inversion is \(I = \frac{1}{2}(O_1+O_2)\), and its power is \(k = |IO_2^2 - r_2^2|\). That is, the circle of center \(I\) and radius \(\sqrt{k}\) is a mid-circle.

When \(r_1 = r_2\) and the two circles \(\mathcal{C}_1\) and \(\mathcal{C}_2\) do not intersect each other, there is no inversion on a circle which swaps these circles. But they can be swapped by an inversion with a negative power; the pole of this inversion is \(I = \frac{1}{2}(O_1+O_2)\), and its power is \(k = -|IO_2^2 - r_2^2|\).

Let’s check this latest claim. In a previous post, I gave a formula to calculate the image of a circle by an inversion on a circle. A more general formula for the image circle \(\mathcal{C}'(O',r')\) of the circle \(\mathcal{C}(O,r)\) by the inversion of pole \(I\) and possibly negative power \(k\), is: \(O' = I + \frac{k}{d}(O-I)\) and \(r' = \left|\frac{k}{d}\right|r\) at condition that \(d := OI^2 - r^2 \neq 0\) (if \(d=0\), the image of \(\mathcal{C}\) is a line).

invertCircle <- function(I, k, circle){
  O <- circle$center; r <- circle$radius
  d <- c(crossprod(O-I)) - r^2
  list(
    center = I + k/d*(O-I),
    radius = abs(k/d)*r
  )
}
# two congruent circles which do not intersect each other
C1 <- list(center = c(1,2), radius = 3)
C2 <- list(center = c(14,15), radius = 3)
# inversion which swaps the two circles
I <- (C1$center + C2$center) / 2
k <- -abs(c(crossprod(I-C2$center) - C2$radius^2))
# check
invertCircle(I, k, C1) # should be C2
## $center
## [1] 14 15
## 
## $radius
## [1] 3
invertCircle(I, k, C2) # should be C1
## $center
## [1] 1 2
## 
## $radius
## [1] 3

Non-congruent case

Now we assume \(r_1 \neq r_2\). We set \(\rho = \frac{r_1}{r_2}\).

Non-intersecting circles

We firstly consider the case when the two circles do not intersect. They can be outside each other, or one of them can contain the other, and we distinguish these two cases. In both cases, there are two inversions which swap the two circles, one with a positive power and the other with a negative power. So the first one defines a mid-circle, and this is the only one.

Case when the circles are outside each other

The inversion with positive power has pole \(I = O_1 - \frac{\rho}{1-\rho}(O_2-O_1)\), and power \(k = \rho|IO_2^2 - r_2^2|\).

The inversion with negative power has pole \(I = O_1 + \frac{\rho}{1+\rho}(O_2-O_1)\), and power \(k = -\rho|IO_2^2 - r_2^2|\).

Here is a picture of the mid-circle:

O1 <- c(0,2); r1 <- 3
O2 <- c(4,5); r2 <- 1
rho <- r1/r2
I <- O1 - rho/(1-rho)*(O2-O1)
k <- rho * abs(c(crossprod(I-O2))-r2^2)
library(plotrix)
opar <- par(mar = c(4,4,1,1))
plot(NULL, asp = 1, xlim = c(-3, 6), ylim = c(-1,6), 
     xlab = NA, ylab = NA)
draw.circle(O1[1], O1[2], r1, lwd = 2)
draw.circle(O2[1], O2[2], r2, lwd = 2)
draw.circle(I[1], I[2], sqrt(k), lwd = 3, border = "red")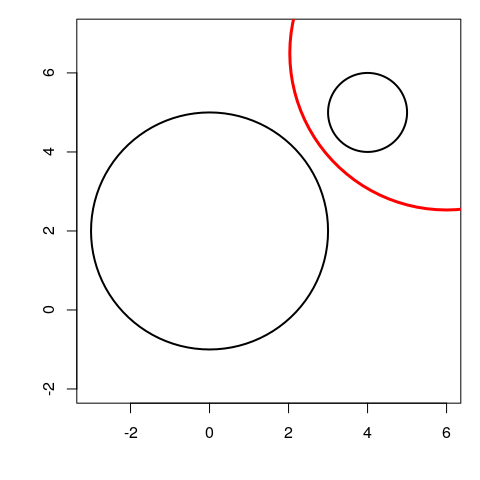

# check
invertCircle(I, k, list(center=O1, radius=r1)) # should be C2
## $center
## [1] 4 5
## 
## $radius
## [1] 1
invertCircle(I, k, list(center=O2, radius=r2)) # should be C1
## $center
## [1] 0 2
## 
## $radius
## [1] 3

Case when one circle contains the other

The inversion with positive power has pole \(I = O_1 + \frac{\rho}{1+\rho}(O_2-O_1)\), and power \(k = \rho|IO_2^2 - r_2^2|\).

The inversion with negative power has pole \(I = O_1 - \frac{\rho}{1-\rho}(O_2-O_1)\), and power \(k = -\rho|IO_2^2 - r_2^2|\).

Here is a picture of the mid-circle:

O1 <- c(0,0); r1 <- 3
O2 <- c(0.7,1); r2 <- 0.7
rho <- r1/r2
I <- O1 + rho/(1+rho)*(O2-O1)
k <- rho * abs(c(crossprod(I-O2))-r2^2)
opar <- par(mar = c(4,4,1,1))
plot(NULL, asp = 1, xlim = c(-3, 3), ylim = c(-3,3), 
     xlab = NA, ylab = NA)
draw.circle(O1[1], O1[2], r1, lwd = 2)
draw.circle(O2[1], O2[2], r2, lwd = 2)
draw.circle(I[1], I[2], sqrt(k), lwd = 3, border = "red")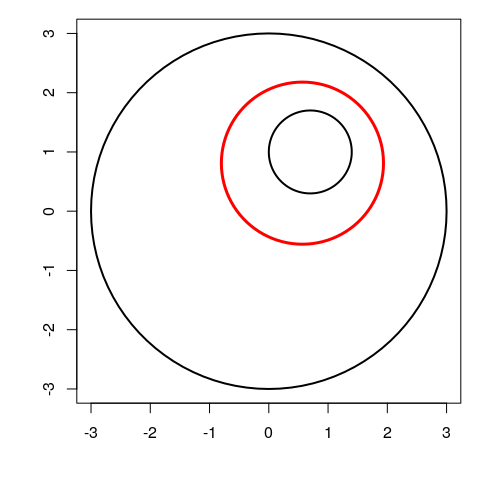

# check
invertCircle(I, k, list(center=O1, radius=r1)) # should be C2
## $center
## [1] 0.7 1.0
## 
## $radius
## [1] 0.7
invertCircle(I, k, list(center=O2, radius=r2)) # should be C1
## $center
## [1] 1.110223e-16 2.220446e-16
## 
## $radius
## [1] 3

Circles intersecting at two points

In this case, there are two mid-circles.
The first inversion has pole \(I = O_1 - \frac{\rho}{1-\rho}(O_2-O_1)\), and power \(k = \rho|IO_2^2 - r_2^2|\). The second inversion has pole \(I = O_1 + \frac{\rho}{1+\rho}(O_2-O_1)\), and power \(k = \rho|IO_2^2 - r_2^2|\).

O1 <- c(5,4); r1 <- 2
O2 <- c(8,5); r2 <- 3
rho <- r1/r2
I1 <- O1 - rho/(1-rho)*(O2-O1)
k1 <- rho * abs(c(crossprod(I1-O2))-r2^2)
I2 <- O1 + rho/(1+rho)*(O2-O1)
k2 <- rho * abs(c(crossprod(I2-O2))-r2^2)
opar <- par(mar = c(4,4,1,1))
plot(NULL, asp = 1, xlim = c(-3, 11), ylim = c(2,8), 
     xlab = NA, ylab = NA)
draw.circle(O1[1], O1[2], r1, lwd = 2)
draw.circle(O2[1], O2[2], r2, lwd = 2)
draw.circle(I1[1], I1[2], sqrt(k1), lwd = 3, border = "red")
draw.circle(I2[1], I2[2], sqrt(k2), lwd = 3, border = "red")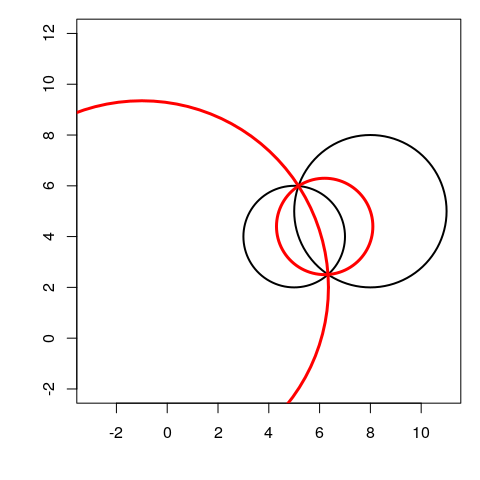

# check
invertCircle(I1, k1, list(center=O1, radius=r1)) # should be C2
## $center
## [1] 8 5
## 
## $radius
## [1] 3
invertCircle(I1, k1, list(center=O2, radius=r2)) # should be C1
## $center
## [1] 5 4
## 
## $radius
## [1] 2
invertCircle(I2, k2, list(center=O1, radius=r1)) # should be C2
## $center
## [1] 8 5
## 
## $radius
## [1] 3
invertCircle(I2, k2, list(center=O2, radius=r2)) # should be C1
## $center
## [1] 5 4
## 
## $radius
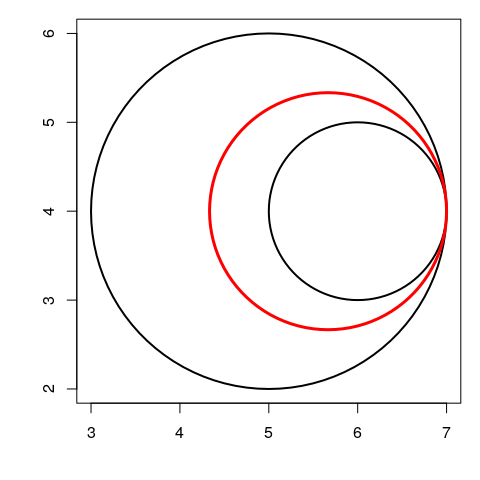
## [1] 2

Tangent circles

In the case when the two circles are tangent, there is only one inversion which swaps the two circles, and this is an inversion on a circle (thus the unique mid-circle).

• If the two circles are externally tangent, this inversion has pole \(I = O_1 - \frac{\rho}{1-\rho}(O_2-O_1)\), and power \(k = \rho|IO_2^2 - r_2^2|\).

O1 <- c(5,4); r1 <- 2
O2 <- c(8,4); r2 <- 1
rho <- r1/r2
I <- O1 - rho/(1-rho)*(O2-O1)
k <- rho * abs(c(crossprod(I-O2))-r2^2)
opar <- par(mar = c(4,4,1,1))
plot(NULL, asp = 1, xlim = c(3, 9), ylim = c(2,6), 
     xlab = NA, ylab = NA)
draw.circle(O1[1], O1[2], r1, lwd = 2)
draw.circle(O2[1], O2[2], r2, lwd = 2)
draw.circle(I[1], I[2], sqrt(k), lwd = 3, border = "red")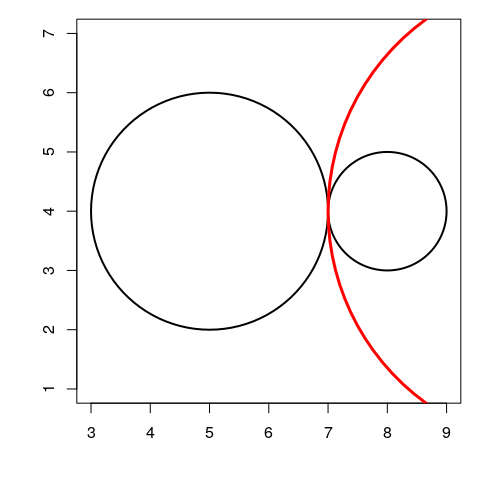

# check
invertCircle(I, k, list(center=O1, radius=r1)) # should be C2
## $center
## [1] 8 4
## 
## $radius
## [1] 1
invertCircle(I, k, list(center=O2, radius=r2)) # should be C1
## $center
## [1] 5 4
## 
## $radius
## [1] 2

• If the two circles are internally tangent, the inversion has pole \(I = O_1 + \frac{\rho}{1+\rho}(O_2-O_1)\), and power \(k = \rho|IO_2^2 - r_2^2|\).

O1 <- c(5,4); r1 <- 2
O2 <- c(6,4); r2 <- 1
rho <- r1/r2
I <- O1 + rho/(1+rho)*(O2-O1)
k <- rho * abs(c(crossprod(I-O2))-r2^2)
opar <- par(mar = c(4,4,1,1))
plot(NULL, asp = 1, xlim = c(3, 7), ylim = c(2,6), 
     xlab = NA, ylab = NA)
draw.circle(O1[1], O1[2], r1, lwd = 2)
draw.circle(O2[1], O2[2], r2, lwd = 2)
draw.circle(I[1], I[2], sqrt(k), lwd = 3, border = "red")

# check
invertCircle(I, k, list(center=O1, radius=r1)) # should be C2
## $center
## [1] 6 4
## 
## $radius
## [1] 1
invertCircle(I, k, list(center=O2, radius=r2)) # should be C1
## $center
## [1] 5 4
## 
## $radius
## [1] 2

par(opar)