Parametric surface with OpenGL in Haskell

In this blog post, I will show how to draw a parametric surface with the Haskell OpenGL library.

We will take as example the following function with two variables \(u\) and \(v\) and depending on a parameter \(n\):

\[ f_n(u,v) = \begin{pmatrix} \sin\Bigl(n v + \dfrac{\pi}{2}\Bigr) \left(\Bigl(1-\dfrac{v}{2\pi}\Bigr)(1 - \cos u) -0.2 \right) \\ \dfrac{4v}{\pi} \Bigl(1-\dfrac{v}{2\pi}\Bigr) \sin u \\ \cos\Bigl(n v + \dfrac{\pi}{2}\Bigr) \left(\Bigl(1-\dfrac{v}{2\pi}\Bigr)(1 - \cos u) +0.2 \right) \end{pmatrix} \] for \(0 \leq u \leq 2\pi\) and \(0 \leq v \leq 2\pi\). It draws a conical spiral (see the images below).

Firslty, we define this function in Haskell:

function :: Double           -- parameter n
         -> Double -> Double -- variables u and v
         -> [Double]         -- result vector
function n u v = [x, y, z]
  where
    x = sin(n*v+0.5*pi) * ((1-0.5*v/pi) * (1-cos u) - 0.2)
    y = 4*v/pi + (1-0.5*v/pi) * sin u
    z = cos(n*v+0.5*pi) * ((1-0.5*v/pi) * (1-cos u) + 0.2)

We will evaluate the function \(f_n\) at the corners of each square of a grid like the one show below:

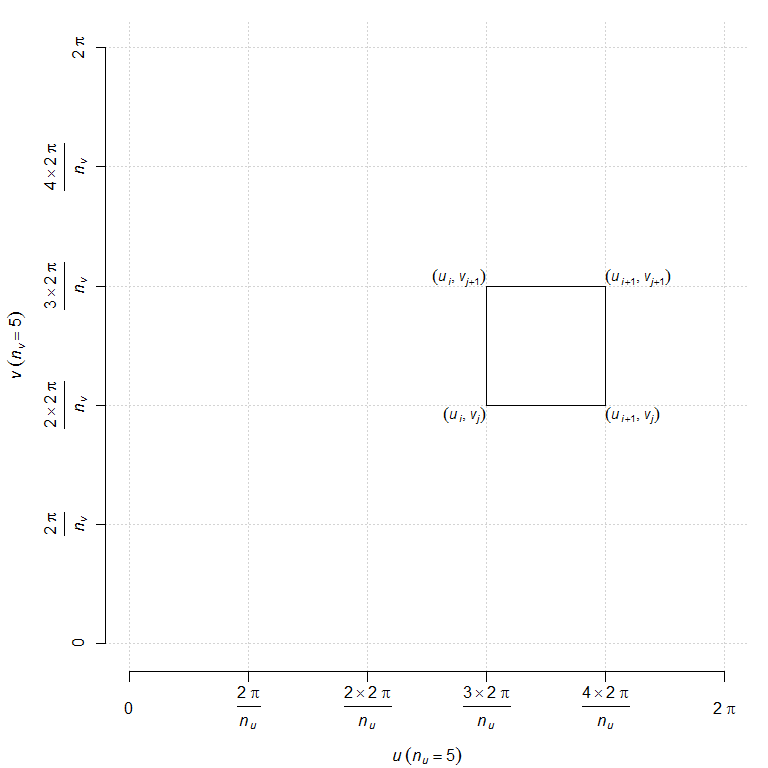
This is done by the Haskell function quad below, which returns a pair made of a four-tuple of Vertex3 and the normal. To get the normal, we use the helper function triangleNormal which computes the cross product.

import Graphics.Rendering.OpenGL.GL (Normal3 (..), Vertex3 (..))

triangleNormal :: Floating a => (Vertex3 a, Vertex3 a, Vertex3 a) -> Normal3 a
triangleNormal (Vertex3 x1 x2 x3, Vertex3 y1 y2 y3, Vertex3 z1 z2 z3) =
  Normal3 (a/norm) (b/norm) (c/norm)
  where
    (a, b, c) = crossProd (y1-x1, y2-x2, y3-x3) (z1-x1, z2-x2, z3-x3)
    crossProd (a1,a2,a3) (b1,b2,b3) = (a2*b3-a3*b2, a3*b1-a1*b3, a1*b2-a2*b1)
    norm = sqrt (a*a + b*b + c*c)


quad :: (Double -> Double -> Double -> [Double]) -- the function
     -> Double                                   -- parameter n
     -> [Double] -> [Double]                     -- sequences of u and v
     -> Int -> Int                               -- indices
     -> ((Vertex3 Double, Vertex3 Double, Vertex3 Double, Vertex3 Double),
          Normal3 Double)
quad f n u_ v_ i j = ((a, b, c, d), norm)
  where
  (a,b,c,d) = ( toVx3 $ f n (u_!!i) (v_!!j)
              , toVx3 $ f n (u_!!i) (v_!!(j+1))
              , toVx3 $ f n (u_!!(i+1)) (v_!!(j+1))
              , toVx3 $ f n (u_!!(i+1)) (v_!!j)    )
  norm = triangleNormal (a, b, c)
  toVx3 x = Vertex3 (x!!0) (x!!1) (x!!2)

Now we compute all the quad’s for two given integers defining the grid:

allQuads :: Int -> Int -- numbers of subdivisions for u and v
         -> Double     -- parameter n
         -> [((Vertex3 Double, Vertex3 Double, Vertex3 Double, Vertex3 Double),
               Normal3 Double)]
allQuads n_u n_v n =
    map (uncurry (quad function n seq_u seq_v))
        [(i,j) | i <- [0 .. n_u-1], j <- [0 .. n_v-1]]
    where
      seq_u,seq_v :: [Double]
      seq_u = [2*pi * frac i n_u | i <- [0 .. n_u]]
      seq_v = [2*pi * frac i n_v | i <- [0 .. n_v]]
      frac :: Int -> Int -> Double
      frac p q = realToFrac p / realToFrac q

Now we make a standard OpenGL program. We allow the user to use the keyboard for some controls: rotating the scene and increasing/decreasing the parameter \(n\).

module ConicalSpiral.ConicalSpiral2 where
import           ConicalSpiral.Data2
import           Data.IORef
import           Graphics.Rendering.OpenGL.GL
import           Graphics.UI.GLUT

white,black,red :: Color4 GLfloat
white      = Color4    1    1    1    1
black      = Color4    0    0    0    1
red        = Color4    1    0    0    1

display :: IORef GLfloat -> IORef GLfloat -> IORef GLfloat -- rotations
        -> IORef GLdouble  -- parameter n
        -> IORef GLdouble  -- zoom
        -> DisplayCallback
display rot1 rot2 rot3 n zoom = do
  clear [ColorBuffer, DepthBuffer]
  n' <- get n
  r1 <- get rot1
  r2 <- get rot2
  r3 <- get rot3
  z <- get zoom
  (_, size) <- get viewport
  let surface = allQuads 200 200 n'
  loadIdentity
  resize z size
  rotate r1 $ Vector3 1 0 0
  rotate r2 $ Vector3 0 1 0
  rotate r3 $ Vector3 0 0 1
  renderPrimitive Quads $ do
    materialDiffuse FrontAndBack $= red
    mapM_ drawQuad surface
  swapBuffers
  where
    drawQuad ((v1,v2,v3,v4),norm) = do
      normal norm
      vertex v1
      vertex v2
      vertex v3
      vertex v4

resize :: Double -> Size -> IO ()
resize zoom s@(Size w h) = do
  viewport $= (Position 0 0, s)
  matrixMode $= Projection
  loadIdentity
  perspective 45.0 (w'/h') 1.0 100.0
  lookAt (Vertex3 0 0 (-15+zoom)) (Vertex3 0 2 0) (Vector3 0 1 0)
  matrixMode $= Modelview 0
  where
    w' = realToFrac w
    h' = realToFrac h

keyboard :: IORef GLfloat -> IORef GLfloat -> IORef GLfloat -- rotations
         -> IORef GLdouble -- parameter n
         -> IORef GLdouble -- zoom
         -> KeyboardCallback
keyboard rot1 rot2 rot3 n zoom c _ =
  case c of
    'b' -> n $~! subtract 0.1
    'n' -> n $~! (+ 0.1)
    'e' -> rot1 $~! subtract 1
    'r' -> rot1 $~! (+1)
    't' -> rot2 $~! subtract 1
    'y' -> rot2 $~! (+1)
    'u' -> rot3 $~! subtract 1
    'i' -> rot3 $~! (+1)
    'm' -> zoom $~! (+1)
    'l' -> zoom $~! subtract 1
    'q' -> leaveMainLoop
    _   -> return ()

idle :: IdleCallback
idle = postRedisplay Nothing

main :: IO ()
main = do
  _ <- getArgsAndInitialize
  _ <- createWindow "Conical Surface"
  windowSize $= Size 500 500
  initialDisplayMode $= [RGBAMode, DoubleBuffered, WithDepthBuffer]
  clearColor $= white
  materialAmbient FrontAndBack $= black
  materialShininess FrontAndBack $= 95
  materialSpecular FrontAndBack $= white
  lighting $= Enabled
  lightModelTwoSide $= Enabled
  light (Light 0) $= Enabled
  position (Light 0) $= Vertex4 0 0 (-100) 1
  ambient (Light 0) $= black
  diffuse (Light 0) $= white
  specular (Light 0) $= white
  depthFunc $= Just Less
  shadeModel $= Smooth
  n <- newIORef 5.0
  rot1 <- newIORef 0.0
  rot2 <- newIORef 0.0
  rot3 <- newIORef 0.0
  zoom <- newIORef 0.0
  displayCallback $= display rot1 rot2 rot3 n zoom
  reshapeCallback $= Just (resize 0)
  keyboardCallback $= Just (keyboard rot1 rot2 rot3 n zoom)
  idleCallback $= Just idle
  putStrLn "*** Haskell OpenGL Conical Spiral ***\n\
        \    To quit, press q.\n\
        \    Scene rotation:\n\
        \        e, r, t, y, u, i\n\
        \    Zoom: l, m\n\
        \    Increase/decrease parameter: n, b \n\
        \"
  mainLoop

And this is the result:

We have chosen to render the conical spiral in red. We can include colors. A possible way to do so is to compute the average value of the quad, normalize it and consider the result as a RGB code:

import Graphics.Rendering.OpenGL.GL (Color4 (..), GLfloat, Vertex3 (..))

type Quad = (Vertex3 Double, Vertex3 Double, Vertex3 Double, Vertex3 Double)

colMeans :: Quad -> (Double, Double, Double)
colMeans quad = (x/m , y/m, z/m)
  where
    (a, b, c, d) = quad
    Vertex3 a1 a2 a3 = a
    Vertex3 b1 b2 b3 = b
    Vertex3 c1 c2 c3 = c
    Vertex3 d1 d2 d3 = d
    x = abs (a1 + b1 + c1 + d1)
    y = abs (a2 + b2 + c2 + d2)
    z = abs (a3 + b3 + c3 + d3)
    m = x + y + z

quadColor :: Quad -> Color4 GLfloat
quadColor quad =
  Color4 (realToFrac x) (realToFrac y) (realToFrac z) 1
  where
    (x,y,z) = colMeans quad

Then, in our display function:

  ......
  renderPrimitive Quads $ mapM_ drawQuad surface
  swapBuffers
  where
    drawQuad ((v1,v2,v3,v4),norm) = do
      materialDiffuse FrontAndBack $= quadColor (v1,v2,v3,v4) 
      normal norm
      vertex v1
      vertex v2
      vertex v3
      vertex v4

And this is the result:

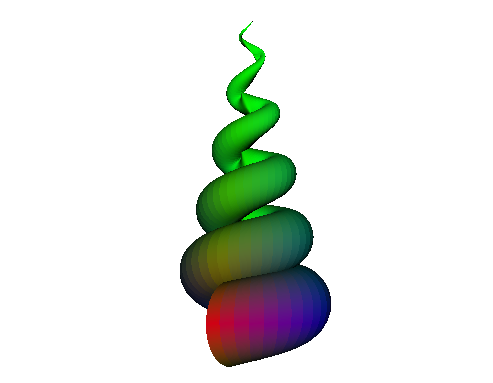
The full code is available in this Github repo.