Drawing a tubular path with Julia

Posted on August 4, 2023 by Stéphane Laurent

I implemented the framed closed curves exposed in this blog post, in Julia and R. In fact it is useless with R, because the rgl function cylinder3d is faster and better.

Here is the Julia implementation:

using LinearAlgebra
using Quaternions
using Meshes

# quaternion corresponding to "the" rotation mapping u to v
function quaternionFromTo(u, v)
  re = √((1.0 + u ⋅ v) / 2.0)
  w = (u × v) / 2.0 / re
  return QuaternionF64(re, w...)
end

# pts: points forming the path
# sides: number of sides of the tube
# radius: tube radius
# twists: number of twists
function closedTube(pts, sides, radius, twists)
  n, _ = size(pts)
  e = [pts[i+1, :] - pts[i, :] for i in 1:(n-1)]
  push!(e, pts[1, :] - pts[n, :])
  tangents = map(normalize, e)
  qtangents = map(tgt -> QuaternionF64(0.0, tgt...), tangents)
  dotproducts = [tangents[i+1, :] ⋅ tangents[i, :] for i in 1:(n-1)]
  a = sqrt.((1 .+ dotproducts) / 2.0)
  V = Vector{Vector{Float64}}(undef, n-1)
  for i in 1:(n-1)
    V[i] = - [imag_part(qtangents[i+1] * qtangents[i])...] / 
      sqrt(2.0 + 2.0*dotproducts[i])
  end
  Qs = [QuaternionF64(a[i], V[i]...) for i in 1:(n-1)]
  # the quaternions psi_k
  Qprodcuts = Vector{QuaternionF64}(undef, n-1)
  Qprodcuts[1] = Qs[1]
  for i in 2:(n-1)
    Qprodcuts[i] = Qs[i] * Qprodcuts[i-1]
  end
  Psi = Vector{QuaternionF64}(undef, n)
  psi0 = quaternionFromTo([1; 0; 0], tangents[1])
  Psi[1] = psi0
  for i in 1:(n-1)
    Psi[i+1] = Qs[i] * Psi[i]
  end
  # angle defect omega 
  init = zeros(Float64, 3)
  init[argmin(tangents[1])] = 1
  N0 = normalize(tangents[1] × init)
  qN0 = QuaternionF64(0.0, N0...)
  qlast = Qprodcuts[n-1]
  qNN = qlast * qN0 * conj(qlast)
  NN = [imag_part(qNN)...]
  x = NN ⋅ N0
  T0 = normalize(NN × N0)
  B0 = T0 × N0
  y = NN ⋅ B0
  omega = atan(y, x) + twists * 2.0 * pi
  # the quaternions psiTilde_k
  norms = map(v -> sqrt(v ⋅ v), e[1:(n-1)])
  s = cumsum([0.0, norms...])
  angles = -omega * s / (2*s[n])
  PsiTilde = Vector{QuaternionF64}(undef, n)
  PsiTilde[1] = Psi[1]
  for i in 2:n
    angle = angles[i]
    PsiTilde[i] = Psi[i] * 
      QuaternionF64(cos(angle), sin(angle), 0.0, 0.0)
  end
  # mesh 
  R = zeros(Float64, 3, sides, n-1)
  Hj = QuaternionF64(0.0, 0.0, 1.0, 0.0)
  for k in 1:sides
    α = (k - 1.0) / sides
    r0 = QuaternionF64(cospi(α), sinpi(α), 0.0, 0.0)
    r1 = r0 * Hj * conj(r0)
    for j in 1:(n-1)
      psi = PsiTilde[j]
      R[:, k, j] = pts[j, :] + 
        radius * [imag_part(psi * r1 * conj(psi))...]
    end
  end
  verts = hcat([R[:, :, i] for i in 1:(n-1)]...)
  points = [verts[:, i] for i in 1:((n-1)*sides)] 
  quads = GridTopology((sides, n-1), (true, true))
  return SimpleMesh([Meshes.Point(pt...) for pt in points], quads)
end

Here is an example, a knot:

using MeshViz
using GLMakie

theta = collect(LinRange(0, 2*pi, 151)[1:150])
knot = 
  [
      [sin.(theta) + 2*sin.(2*theta)]
    , [2*sin.(3*theta)]
    , [cos.(theta) - 2*cos.(2*theta)]
  ]

mesh = closedTube(knot, 60, 0.35, 0)
viz(mesh)

The current version of MeshViz always adds normals to the meshes, so we can’t correctly see what happens if we only set a couple of sides and if we use some twists. So let’s see what this gives with the R version, with four sides and two twists:

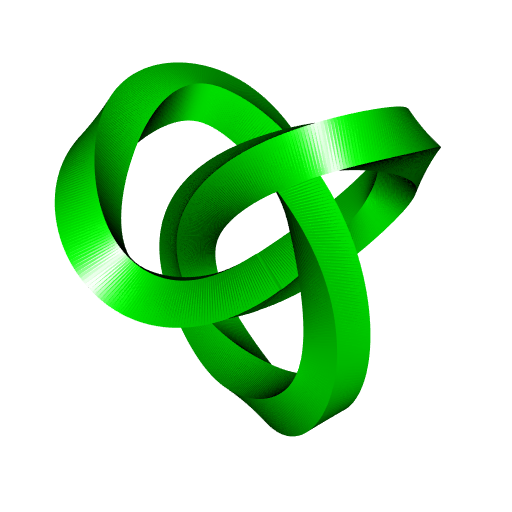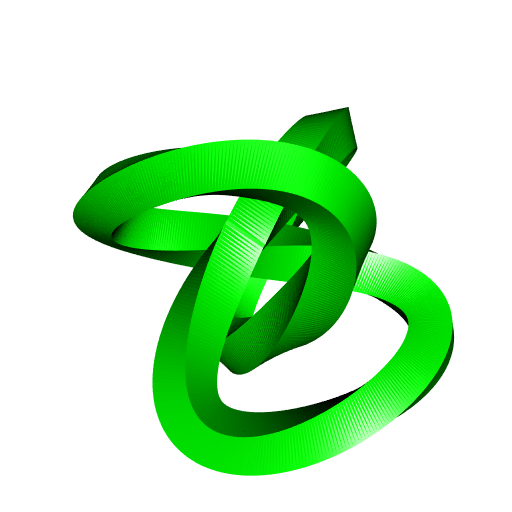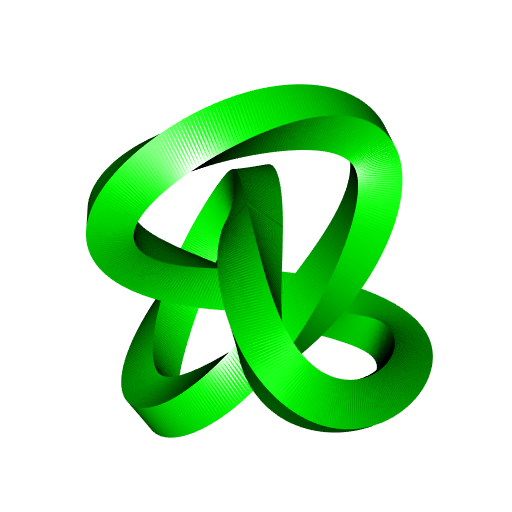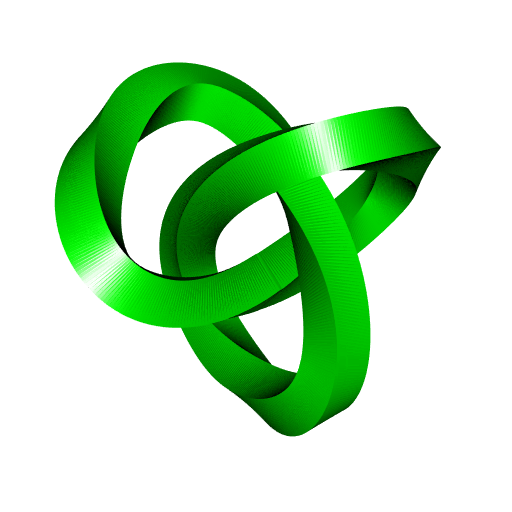
Below is the R code. But again, don’t use it, use rgl::cylinder3d instead.

library(onion)
library(rgl)

closedTubeMesh <- function(pts, nsides, epsilon, twist = 0) {
  n <- nrow(pts)
  # tangents
  e <- rbind(
    t(vapply(1L:(n-1L), function(i) pts[i+1L, ]-pts[i, ], numeric(3L))),
    pts[1L, ]-pts[n, ]
  )
  nrms <- sqrt(apply(e, 1L, crossprod))
  Tgs <- e / nrms
  Tgs_quat <- as.quaternion(rbind(0, t(Tgs)))
  # the quaternions q
  sprods <- vapply(
    1L:(n-1L), function(i) c(crossprod(Tgs[i+1L, ], Tgs[i, ])), numeric(1L)
  )
  a <- sqrt((1 + sprods) / 2)
  v <- quaternion(length.out = n-1L)
  for(i in 1L:(n-1L)) {
    v[i] <- -1 / sqrt(2 + 2*sprods[i]) * Im(Tgs_quat[i+1L] * Tgs_quat[i])
  }
  q <- a + v
  # the psi_k
  qpr <- Conj(onion_cumprod(Conj(q))) 
  Psi <- quaternion(length.out = n)
  psi0 <- cgalMeshes:::quaternionFromTo(c(1, 0, 0), Tgs[1L, ])
  Psi[1L] <- psi0
  for(i in 1L:(n-1L)) {
    Psi[i+1L] <- qpr[i] * psi0
  }
  # omega (angle defect)
  init <- c(0, 0, 0)
  init[which.min(abs(Tgs[1L, ]))] <- 1
  N0 <- cgalMeshes::crossProduct(Tgs[1L, ], init)
  N0 <- N0 / sqrt(c(crossprod(N0)))
  N0_quat <- as.quaternion(c(0, N0), single = TRUE)
  qN <- qpr[n-1L]
  NN_quat <- qN * N0_quat * Conj(qN)
  NN <- as.numeric(NN_quat)[-1L]
  x <- c(crossprod(NN, N0))
  T0 <- cgalMeshes::crossProduct(NN, N0)
  T0 <- T0 / sqrt(c(crossprod(T0)))
  B0 <- cgalMeshes::crossProduct(T0, N0) 
  y <- c(crossprod(NN, B0)) # x^2+y^2=1
  omega <- atan2(y, x) + twist*2*pi
  # the quaternions psiTilde_k
  s <- cumsum(c(0, apply(e[-n, ], 1L, crossprod)))
  L <- s[n]
  angles <- -omega * s / (2*L)
  PsiTilde <- quaternion(length.out = n)
  PsiTilde[1L] <- Psi[1L]
  for(i in 2L:n) {
    a <- angles[i]
    PsiTilde[i] <- 
      Psi[i] * as.quaternion(c(cos(a), sin(a), 0, 0), single = TRUE)
  }
  # the mesh
  nu <- n
  uperiodic <- TRUE
  u_ <- 1L:nu
  vperiodic <- TRUE
  nv <- as.integer(nsides)
  v_ <- 1L:nv
  R <- array(NA_real_, dim = c(3L, nv, nu))
  for(k in 1L:nv) {
    a <- (k - 1L) / nv
    r0 <- as.quaternion(c(cospi(a), sinpi(a), 0, 0), single = TRUE)
    r1 <- r0 * Hj * Conj(r0)
    for(j in 1L:nu) {
      psi <- PsiTilde[j]
      R[, k, j] <- 
        pts[j, ] + epsilon * as.numeric(psi * r1 * Conj(psi))[-1L]
    }
  }
  vs <- matrix(R, nrow = 3L, ncol = nu*nv)
  tris <- cgalMeshes:::meshTopology(nu, nv, uperiodic, vperiodic)
  tmesh3d(
    vertices    = vs,
    indices     = tris,
    homogeneous = FALSE
  )
}

################################################################################
theta <- seq(0, 2*pi, length.out = 751L)[-1L]
knot <- cbind(
  sin(theta) + 2*sin(2*theta), 
  2*sin(3*theta), 
  cos(theta) - 2*cos(2*theta)
)
mesh <- closedTubeMesh(knot, nsides = 4, epsilon = 0.55, twist = 2)
shade3d(mesh, color = "green")