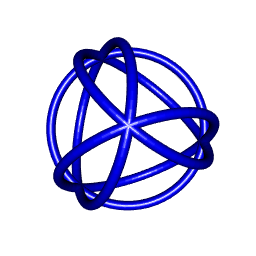
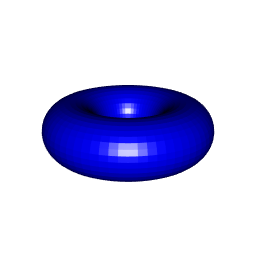
Drawing a torus with rgl

The following function creates a torus as a mesh3d object, which can be drawn with the rgl package.

# R: major radius
# r: minor radius
# S: number of segments for the major ring
# s: number of segments for the minor ring
# arc: the arc to draw
library(rgl)
createTorusMesh <- function(R=1, r=0.25, S=64, s=32, arc=2*pi){
  vertices <- indices <- NULL
  for (j in 0:s) {
    for (i in 0:S) {
      u <- i / S * arc
      v <- j / s * 2*pi
      vertex <- c(
        (R + r*cos(v)) * cos(u),
        (R + r*cos(v)) * sin(u),
        r * sin(v)
      )
      vertices <- cbind(vertices, vertex)
    }
  }
  for (j in 1:s) {
    for (i in 1:S) {
      a <- (S + 1) * j + i 
      b <- (S + 1) * (j - 1) + i 
      c <- (S + 1) * (j - 1) + i + 1
      d <- (S + 1) * j + i + 1
      indices <- cbind(indices, c(a,b,d), c(b,c,d))
    }
  }
  tmesh3d(rbind(vertices,1), indices)
}

torus <- createTorusMesh(R=2, r=1)
shade3d(torus, color="blue")

Denote by \(O\) the center of the torus and by \(R\) its major radius. The equator of this torus (circle of center \(O\) and radius \(R\)) lies in the \(xy\)-plane (the plane \(z=0\)).

Now we are going to give a method to draw a torus such that its equator passes by three given points. This will be done with the help of the transform3d function of the rgl package. Thus, the key element to construct is the transformation matrix.

Firstly, we write a function which returns the center and the radius of a circle passing by three given points in the 3D space. This is the function circleCenterAndRadius below. The plane3pts function is an helper function which returns the equation of the plane passing by three points.

# plane passing by points p1, p2, p3 #
plane3pts <- function(p1,p2,p3){ 
    xcoef = (p1[2]-p2[2])*(p2[3]-p3[3])-(p1[3]-p2[3])*(p2[2]-p3[2]);
    ycoef = (p1[3]-p2[3])*(p2[1]-p3[1])-(p1[1]-p2[1])*(p2[3]-p3[3]);
    zcoef = (p1[1]-p2[1])*(p2[2]-p3[2])-(p1[2]-p2[2])*(p2[1]-p3[1]);
    offset = p1[1]*xcoef + p1[2]*ycoef + p1[3]*zcoef; 
    c(xcoef, ycoef, zcoef, offset)
}

# center, radius and normal of the circle passing by three points #
circleCenterAndRadius <- function(p1,p2,p3){
    p12 <- (p1+p2)/2
    p23 <- (p2+p3)/2
    v12 <- p2-p1
    v23 <- p3-p2
    plane <- plane3pts(p1,p2,p3)
    A <- rbind(plane[1:3],v12,v23)
    b <- c(plane[4], sum(p12*v12), sum(p23*v23))
    center <- c(solve(A) %*% b)
    r <- sqrt(c(crossprod(p1-center)))
    list(center=center, radius=r, normal=plane[1:3])
}

Note that circleCenterAndRadius actually returns not only the center and the radius, but also a vector perpendicular to the plane of the circle.

Now, we are ready to write the function which returns the desired transformation matrix.

transfoMatrix <- function(p1,p2,p3){
  crn <- circleCenterAndRadius(p1,p2,p3)
  center <- crn$center
  radius <- crn$radius
  normal <- crn$normal
  measure <- sqrt(normal[1]^2+normal[2]^2+normal[3]^2)
  normal <- normal/measure
  s <- sqrt(normal[1]^2+normal[2]^2) # TODO: case s=0
  u <- c(normal[2]/s, -normal[1]/s, 0)
  v <- geometry::extprod3d(normal, u)
  m <- rbind(cbind(u, v, normal, center), c(0,0,0,1)) 
  list(matrix=t(m), radius=radius)
}

Our function transfoMatrix also returns a radius, the major radius of the desired torus.

Let us test it now.

library(rgl)
# our three points
p1 = c(1,-1,1)
p2 = c(2,1,2)
p3 = c(2,-2,-3)
# get the transformation matrix and the radius
mr <- transfoMatrix(p1,p2,p3)
tmesh0 <- createTorusMesh(R=mr$radius, r=0.1)
tmesh <- transform3d(tmesh0, mr$matrix)
# draw the torus
shade3d(tmesh, color="blue")
# and draw a triangle to check
triangles3d(rbind(p1,p2,p3), color="red")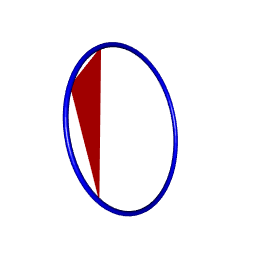

It works. So let’s play with it now.

tetrahedron <- tetrahedron3d()[c("vb","it")]
vertices <- tetrahedron$vb[1:3,]
triangles <- tetrahedron$it
#
p1 <- vertices[,triangles[1,1]]
p2 <- vertices[,triangles[2,1]]
p3 <- vertices[,triangles[3,1]]
mr <- transfoMatrix(p1,p2,p3)
tmesh <- transform3d(createTorusMesh(R=mr$radius, r=0.1), mr$matrix)
shade3d(tmesh, color="blue")
#
p1 <- vertices[,triangles[1,2]]
p2 <- vertices[,triangles[2,2]]
p3 <- vertices[,triangles[3,2]]
mr <- transfoMatrix(p1,p2,p3)
tmesh <- transform3d(createTorusMesh(R=mr$radius, r=0.1), mr$matrix)
shade3d(tmesh, color="blue")
#
p1 <- vertices[,triangles[1,3]]
p2 <- vertices[,triangles[2,3]]
p3 <- vertices[,triangles[3,3]]
mr <- transfoMatrix(p1,p2,p3)
tmesh <- transform3d(createTorusMesh(R=mr$radius, r=0.1), mr$matrix)
shade3d(tmesh, color="blue")
#
p1 <- vertices[,triangles[1,4]]
p2 <- vertices[,triangles[2,4]]
p3 <- vertices[,triangles[3,4]]
mr <- transfoMatrix(p1,p2,p3)
tmesh <- transform3d(createTorusMesh(R=mr$radius, r=0.1), mr$matrix)
shade3d(tmesh, color="blue")