Rbloggers
Standard error Timely portfolio
ENHANCE DATA
Fronkonstin

Parametric surface in Haskell OpenGL, with surface normals

Posted on October 23, 2018 by Stéphane Laurent
Tags: haskell, graphics, opengl

Similarly to a previous post, I will show here how to draw a parametric surface with the Haskell OpenGL library, but this time we will include the surface normal at each vertex.

As the example of a surface, I take the stereographic projection of a Hopf torus. The parameterization is given by the function defined as follows in Haskell:

for \(0 \leq u < 2\pi\) and \(0 \leq v < 2\pi\).

We will evaluate this function at the vertices of a grid like the one shown below (we will see later why we show the six red triangles on this picture):

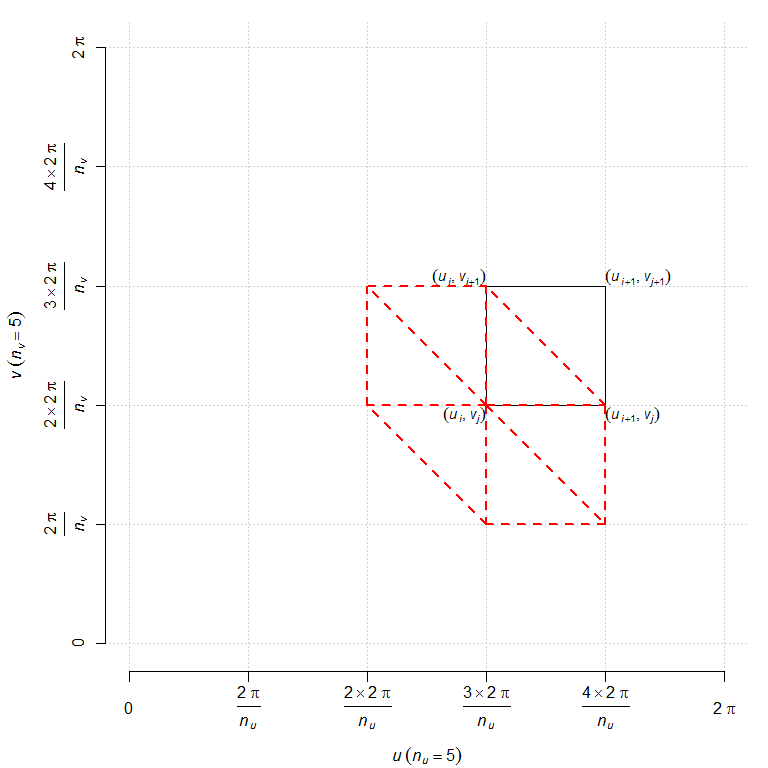
We write a function that evaluates the values of a parametrization at the point of this grid and put them in an array:

These values are the surface vertices. Now, we write a function that approximates the surface normal at vertex \((i,j)\). This normal approximately is the average of the normals of the six triangles incident to the vertex.

Now we write a function that takes the array of surface vertices as input and returns an array containing the surface normals:

Let’s say that a surface triangle whose each vertex is attached to the
corresponding surface normal is a n-triangle. To each vertex \((i,j)\), we associate two n-triangles: the lower n-triangle for vertices \((i,j)\)-\((i+1,j)\)-\((i,j+1)\) and the upper n-triangle for vertices \((i+1,j+1)\)-\((i,j+1)\)-\((i+1,j)\). We write a function that takes as input the two arrays (vertices and normals), an index \((i,j)\), and that returns the two n-triangles:

Finally, we write a function returning the list of all pairs of n-triangles:

Done. It remains to write the OpenGL side:

import Data.IORef
import Graphics.Rendering.OpenGL.GL
import Graphics.UI.GLUT

hopfTorus :: [(NTriangle,NTriangle)]
hopfTorus = allTriangles (400,400)

data Context = Context
    {
      contextRot1      :: IORef GLfloat
    , contextRot2      :: IORef GLfloat
    , contextRot3      :: IORef GLfloat
    , contextTriangles :: IORef [(NTriangle,NTriangle)]
    }

white,black,pink :: Color4 GLfloat
white      = Color4    1   1   1    1
black      = Color4    0   0   0    1
pink       = Color4    1   0   0.5  1

display :: Context -> IORef GLdouble -> DisplayCallback
display context zoom alpha = do
  clear [ColorBuffer, DepthBuffer]
  r1 <- get (contextRot1 context)
  r2 <- get (contextRot2 context)
  r3 <- get (contextRot3 context)
  ntriangles <- get (contextTriangles context)
  let ntriangles' = unzip ntriangles
      lowerTriangles = fst ntriangles'
      upperTriangles = snd ntriangles'
  z <- get zoom
  loadIdentity
  (_, size) <- get viewport
  resize z size
  rotate r1 $ Vector3 1 0 0
  rotate r2 $ Vector3 0 1 0
  rotate r3 $ Vector3 0 0 1
  renderPrimitive Triangles $ mapM_ drawTriangle lowerTriangles
  renderPrimitive Triangles $ mapM_ drawTriangle lowerTriangles
  swapBuffers
  where
    drawTriangle ((v1,n1),(v2,n2),(v3,n3)) = do
      materialDiffuse Front $= pink
      normal n1
      vertex v1
      normal n2
      vertex v2
      normal n3
      vertex v3

resize :: GLdouble -> Size -> IO ()
resize zoom s@(Size w h) = do
  viewport $= (Position 0 0, s)
  matrixMode $= Projection
  loadIdentity
  perspective 45.0 (realToFrac w / realToFrac h) 1.0 100.0
  lookAt (Vertex3 0 0 (24+zoom)) (Vertex3 0 0 0) (Vector3 0 1 0)
  matrixMode $= Modelview 0

keyboard :: IORef GLfloat -> IORef GLfloat -> IORef GLfloat -- rotations
         -> IORef GLdouble -- zoom
         -> IORef [(NTriangle,NTriangle)]
         -> KeyboardCallback
keyboard rot1 rot2 rot3 zoom triangles c _ = do
  case c of
    'e' -> rot1 $~! subtract 2
    'r' -> rot1 $~! (+2)
    't' -> rot2 $~! subtract 2
    'y' -> rot2 $~! (+2)
    'u' -> rot3 $~! subtract 2
    'i' -> rot3 $~! (+2)
    'm' -> zoom $~! (+0.1)
    'l' -> zoom $~! subtract 0.1
    'q' -> leaveMainLoop
    _   -> return ()
  postRedisplay Nothing

main :: IO ()
main = do
  _ <- getArgsAndInitialize
  _ <- createWindow "Hopf torus"
  windowSize $= Size 500 500
  initialDisplayMode $= [RGBAMode, DoubleBuffered, WithDepthBuffer]
  clearColor $= black
  materialAmbient Front $= black
  lighting $= Enabled
  light (Light 0) $= Enabled
  position (Light 0) $= Vertex4 0 0 (-1000) 1
  ambient (Light 0) $= white
  diffuse (Light 0) $= white
  specular (Light 0) $= white
  depthFunc $= Just Less
  shadeModel $= Smooth
  rot1 <- newIORef 0.0
  rot2 <- newIORef 0.0
  rot3 <- newIORef 0.0
  zoom <- newIORef 0.0
  nlobes' <- newIORef nlobes
  hopfTorus' <- newIORef hopfTorus
  displayCallback $= display Context {contextRot1 = rot1,
                                      contextRot2 = rot2,
                                      contextRot3 = rot3,
                                      contextTriangles = hopfTorus'}
                             zoom 
  reshapeCallback $= Just (resize 0)
  keyboardCallback $= Just (keyboard rot1 rot2 rot3 zoom hopfTorus')
  idleCallback $= Nothing
  putStrLn "*** Hopf torus ***\n\
        \    To quit, press q.\n\
        \    Scene rotation: e, r, t, y, u, i\n\
        \    Zoom: l, m\n\
        \"
  mainLoop

And this is the result:

The full code is available in this Github repo.