Drawing a torus with Julia

Posted on December 15, 2022 by Stéphane Laurent

I already showed how to draw a torus whose equator passes through three given points with three.js, Asymptote, R, POV-Ray, and Haskell. Here I have a method for Python, using PyVista, but it is a bit useless because once you know how to draw a circular path passing through three points you can “tubify” it with PyVista, that is to say you can add a radius to the path. Similarly, you can do that with the R package rgl by using the cylinder3d function.

Now I want to show how to do that with Julia. I’m using the Meshes package because I find it easy to use.

Here is the code:

using LinearAlgebra
using Meshes

# plane passing by points p1, p2, p3 #
function plane3pts(p1, p2, p3)
  normal = LinearAlgebra.cross(p2 - p1, p3 - p1)
  if LinearAlgebra.norm_sqr(normal) == 0
    error("The three points are colinear.")
  end
  offset = LinearAlgebra.dot(Meshes.coordinates(p1), normal)
  return (normal = normal, offset = offset)
end

# center, radius and normal of the circle passing by three points #
function circleCenterAndRadius(p1, p2, p3)
  v12 = p2 - p1
  v13 = p3 - p1
  p12 = Meshes.coordinates(p1 + v12/2)
  p13 = Meshes.coordinates(p1 + v13/2)
  normal, offset = plane3pts(p1, p2, p3)
  A = transpose(hcat(normal, v12, v13))
  b = [
    offset, 
    LinearAlgebra.dot(p12, v12), 
    LinearAlgebra.dot(p13, v13)
  ]
  center = Meshes.Point(inv(A) * b)
  r = LinearAlgebra.norm2(p1 - center)
  return (center = center, radius = r, normal = normal)
end

# key transformation #
function keyTransform(p1, p2, p3)
  center, radius, normal = circleCenterAndRadius(p1, p2, p3)
  normal = normal / LinearAlgebra.norm2(normal)
  s = sqrt(normal[1]^2 + normal[2]^2) 
  if s == 0
    return (matrix = I, center = center, radius = radius)
  end
  u = [normal[2] / s, -normal[1] / s, 0]
  v = LinearAlgebra.cross(normal, u)
  R = hcat(u, v, normal)
  return (rotMatrix = R, center = center, radius = radius)
end

"""
    torusMesh(R, r; nu = 50, nv = 30)

Mesh of a torus with major radius `R` and minor radius `r`, 
with the z-axis as its axis of rotation and the xy-plane as its 
equatorial plane. 

# Arguments
- `R`: major radius
- `r`: minor radius
- `nu`, `nv`: numbers of subdivisions

"""
function torusMesh(R, r; nu = 50, nv = 30)
  kxy = R^2 - r^2
  kz = sqrt(kxy) * r
  s = sqrt(kxy) / r 
  u_ = LinRange(-s*pi, s*pi, nu)
  v_ = LinRange(-pi, pi, nv)
  points = [Meshes.Point(
      [kxy * sin(u/s), kxy * cos(u/s), kz * sin(v)] / (R - r*cos(v))
    ) for u in u_ for v in v_
  ]
  topo = Meshes.GridTopology((nv, nu), (true, true))
  return Meshes.SimpleMesh(points, topo)
end

"""
    torusMesh(r, p1, p2, p3; nu = 50, nv = 30)

Mesh of a torus whose equator passes through three given points.

# Arguments
- `r`: minor radius
- `p1`, `p2`, `p3`: the three points
- `nu`, `nv`: numbers of subdivisions

"""
function torusMesh(r, p1, p2, p3; nu = 50, nv = 30)
  M, center, R = keyTransform(p1, p2, p3)
  mesh = torusMesh(R, r; nu = nu, nv = nv)
  vertices = [
    center + Meshes.Vec3(M * Meshes.coordinates(v)) 
    for v in Meshes.vertices(mesh)
  ]
  return Meshes.SimpleMesh(vertices, Meshes.topology(mesh))
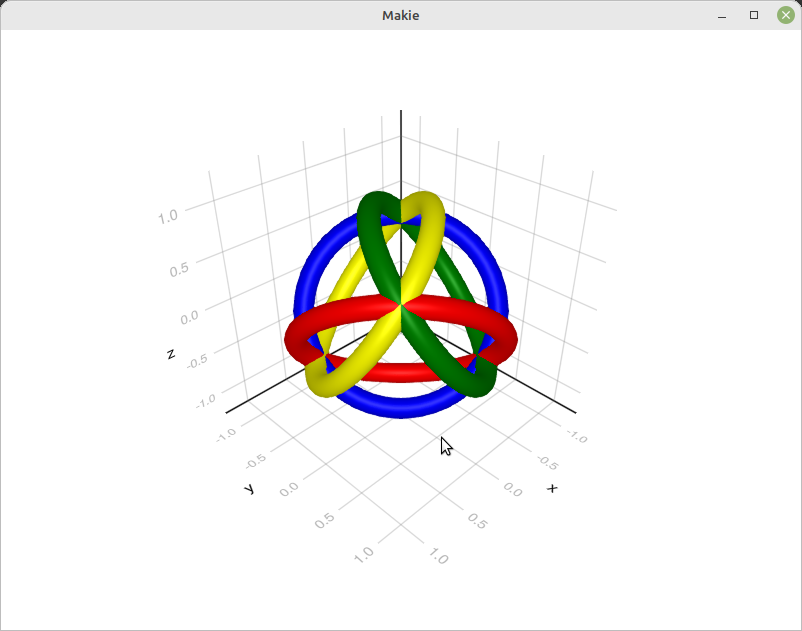
end

And an example:

using MeshViz

a = 1 / sqrt(3)
p1 = [ a, -a, -a]
p2 = [ a,  a,  a]
p3 = [-a, -a,  a]
p4 = [-a,  a, -a]

mesh1 = torusMesh(0.1, p1, p2, p3)
mesh2 = torusMesh(0.1, p1, p2, p4)
mesh3 = torusMesh(0.1, p1, p3, p4)
mesh4 = torusMesh(0.1, p2, p3, p4)

function draw()
  MeshViz.viz!(mesh2; color = :red)
  MeshViz.viz!(mesh3; color = :blue)
  MeshViz.viz!(mesh4; color = :green)
end

MeshViz.viz(mesh1; color=:yellow)
draw()